La dyscalculie

-

 

Si le terme dyscalculie, qui signifie littéralement “difficultés à calculer”, a été créé dans les années 1940, ce n’est qu’en 1974 qu’un scientifique Tchécoslovaque, Ladislav Kosc, le définit de manière plus précise et contribue à le populariser. Cependant, la définition de la dyscalculie reste encore floue à l’heure actuelle, et le diagnostic est souvent supplanté dans la littérature scientifique par des termes proches, comme “difficultés arithmétiques”, “difficultés mathématiques”, ou encore “trouble de l’apprentissage des mathématiques”. Ces nombreuses appellations traduisent des délimitations légèrement différentes, et donc probablement des difficultés d’origines et de natures différentes. La notion même de dyscalculie est donc relativement floue à l’heure actuelle. Cela peut s’expliquer par la difficulté à caractériser ce trouble complexe, multifactoriel, ainsi qu’un relatif désintérêt pendant de nombreuses années de la recherche sur ce sujet. Heureusement, cela est en train de changer, et on peut tenter de dessiner les contours de ce trouble, ses origines et les prises en charges possibles. C’est ce que nous allons tenter de faire dans cet article.

La dyscalculie fait partie d’un vaste ensemble diagnostique, les troubles des apprentissages, qui regroupent de nombreux troubles “dys”, comme la dyslexie ou la dysgraphie/dysorthographie. Ces troubles traduisent des difficultés significatives des élèves à acquérir certains savoirs fondamentaux, comme l’écriture, la lecture ou le calcul. Ces difficultés, par définitions, ne proviennent pas de carences sur le plan éducatif ou pédagogique : elles sont inhérentes à l’enfant, avec une influence importante de prédispositions génétiques. Elles ne sont de plus pas liées à l’intelligence de l’enfant. En effet, il apparait normal et instinctif qu’en enfant avec un retard intellectuel ait des difficultés pour acquérir les bases du calcul : dans ce cas-là, on ne pourra pas parler de dyscalculie car les difficultés s’expliquent par le retard intellectuel, et non par une atteinte spécifique de l’apprentissage du calcul. On ne parlera pas plus de dyscalculie en cas de trouble visuel ou auditif –sur le même raisonnement, une surdité ou une cécité peuvent expliquer des difficultés d’acquisitions scolaires. La CIM-10 exclut aussi du diagnostic de dyscalculie les enfants souffrant de dyslexie, car dans cette approche la dyscalculie est conçue comme secondaire aux difficultés de lecture –dans cette approche, le traitement de la dyslexie corrige la dyscalculie.

Selon les classifications internationales, la dyscalculie concerne donc par définition des enfants avec un QI normal, sans déficit sensoriel ni dyslexie, et bénéficiant d’une scolarité adaptée.

Les premières divergences apparaissent lorsqu’on essaye de caractériser la nature et l’amplitude des difficultés liées à la dyscalculie. Les classifications internationales comme la CIM-10 ou le DSM se basent sur des résultats à des tests standardisés, mais le seuil qu’elle retiennent sont différentes : 2 écarts-types pour la CIM-10, contre 1.5 voire 1 écart-type pour le DSM. La nature même des déficits est débattue : certains scientifiques définissent la dyscalculie comme un trouble de l’apprentissage de l’arithmétique (la manipulation des nombres), alors que d’autres situent le déficit initial plus en amont, dès les aptitudes numériques (le savoir conceptuel et la représentation des nombres). Cette distinction est importante car le tableau clinique présenté et l’évolution des enfants souffrant de troubles de l’arithmétique semble très différent de ceux souffrant d’un déficit plus global des aptitudes mathématiques.

Dans cet article, nous nous référerons à la définition anglaise, qui décrit les enfants dyscalculiques avec des “difficultés à comprendre les concepts numériques simples, a compréhension intuitive des nombres, avec des difficultés pour apprendre les faits numériques et les procédures arithmétiques”. Il s’agit donc d’une définition relativement large.



La dyscalculie, comme les autres troubles du neurodéveloppement (TND), est caractérisée par la grande fréquence de troubles comorbides. C’est particulièrement le cas avec la dyslexie, qui pourrait toucher la moitié des enfants dycalculiques, les troubles du langage ou la dysorthographie. Cette notion de comorbidité est importante car les enfants avec plusieurs troubles dys sont en moyenne plus en difficultés, et leur pronostic est moins bon, comparativement aux enfants avec une dyscalculie isolée. Les troubles comorbides provoquent de plus à une hétérogénéité importante des enfants avec dyscalculie : il n’existe pas une dyscalculie, mais plusieurs !


Quelles étiologies ?

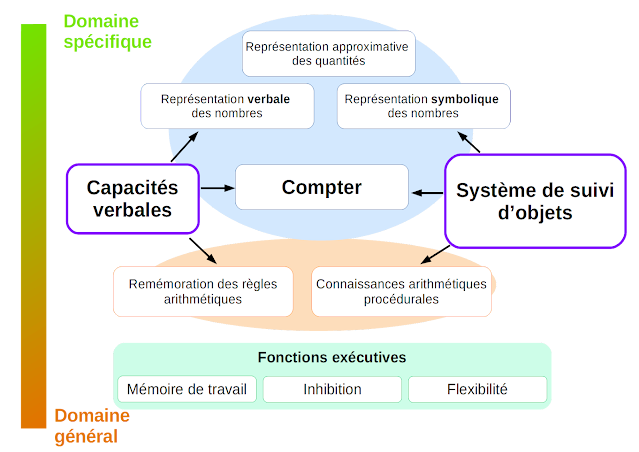
A l’instar de l’acquisition classique des capacités mathématiques, les mécanismes cognitifs potentiels de la dyscalculie peuvent être divisés en deux grands courants : d’une part, certains avancent la prédominance des capacités cognitives spécifiques (la représentation symbolique du nombre, le sens approximatif des quantités, etc.), alors que d’autres pensent que c’est un déficit de fonctions plus générales qui prédominent (et en premier lieu les fonctions exécutives). Ces deux approches ne sont pas exclusives : elles peuvent s’intégrer dans différents profils de patients dyscalculiques (certains à cause de difficultés exécutives, d’autres dans la représentation symbolique des nombres, par exemple), ou de cumuler chez un même patient (par exemple, un patient avec un TDAH, et donc des difficultés exécutives, associé à une difficulté précoce dans le sens approximatif des nombres).


Les aptitudes mathématiques reposent sur de nombreux processus cognitifs, dont certains leur sont spécifiques (en vert), et d'autres sont impliqués dans de nombreux autres domaines (en orange).

De nombreux travaux ont étudié les aptitudes arithmétiques (les opérations sur les nombres comme l’addition ou la soustraction, apprises tôt à l’école primaire) des patients dyscalculiques. D’une part, ces données mettent en évidence la persistance de stratégies immatures dans la résolution de ces opérations. Normalement, au cours des premières années de primaire, les élèves complexifient progressivement les stratégies de résolution des additions : au début, ils comptent depuis le début (pour faire 3+2, ils comptent 1, 2, 3, 4, 5), puis ils ont tendance à compter à partir du 2ème terme (2, 3, 4, 5), puis à partir du plus grand des deux termes (3, 4, 5). Les enfants dyscalculiques ont tendance à continuer d’utiliser les stratégies primitives, et sont en difficulté pour diversifier leurs stratégies de réponse.

Une caractéristique importante de la dyscalculie est la difficulté à stocker puis réutiliser les faits numériques en mémoire. Si nous reprenons l’exemple ci-dessus (3+2), vous n’avez pas eu à faire le calcul pour trouver le résultat : ce dernier était présent en mémoire et vous avez juste eu à le “repécher” pour trouver la réponse. Cette capacité est normalement acquise en cours de CE2. Les études montrent que les élèves dyscalculiques sont en difficulté pour constituer ce répertoire de données numériques, ce qui a évidemment un retentissement sur les calculs simples (il faut refaire mentalement le calcul) que pour la suite des acquisitions (calculs complexes, résolution de problèmes).


Les fonctions cognitives essentielles aux aptitudes mathématiques peuvent leur être spécifiques, ou non (axe vertical à gauche). Elles peuvent concerner les aptitudes numériques (bleu) ou arithmétiques (orange). Les fonctions exécutives (vert) ont une fonction essentielle aux aptitudes mathématiques, bien qu'elles ne leur soient pas spécifiques).

Concernant les fonctions générales, la dyscalculie est régulièrement associée à des difficultés en mémoire de travail (équivalent de la RAM de votre ordinateur, qui permet de maintenir des informations disponibles en mémoire à court terme, pour être utilisée par le processeur). On peut le comprendre intuitivement, la mémoire de travail est essentielle aux opérations arithmétiques, même les plus simples : pour résoudre 2+3, il faut pouvoir garder en mémoire le chiffre initial et précédant pour compter jusqu’à 5 (et c’est évidemment d’autant plus impliqué que le calcul est complexe). Cependant, certains chercheurs suggèrent que le déficit initial ne concerne pas directement la mémoire de travail, mais serait en partie secondaire à la lenteur importante des enfants dans les tâches de résolutions de calcul. En effet, la mémoire de travail reste une mémoire à court terme, qui nous permet de retenir brièvement une information. Si le calcul est devenu trop long (car trop compliqué à réaliser), cela pourrait aboutir à une perte de l’information en mémoire, et donc une erreur de calcul.

Nous l’avions évoqué plus haut, les difficultés rencontrées par les élèves dyscalculiques ne relèvent pas seulement de la sphère arithmétique, mais aussi numérique. Ainsi, ces enfants sont en difficultés très précocement, par exemple dans l’acquisition des représentations symboliques des nombres (faire le lien entre une quantité et sa représentation abstraite – 2 pommes avec le chiffre 2), ou encore dans l’acquisition de la chaîne verbale (le fait de placer les nombres dans le bon ordre). Encore plus précocement, c’est les systèmes primitifs d’évaluation précise des petites quantités et approximative des grandes quantités qui peuvent être déficitaires. Par exemple, leur système de suivi d’objets, qui permet d’identifier et de dénombrer précisément un faible nombre d’objets dans son environnement, normalement efficient très tôt dans le développement de l’enfant, fonctionne moins bien chez les enfants dyscalculiques. Ces difficultés se matérialisent par exemple mais un temps de réponse plus grand lorsqu’on leur demande de dénombrer en un coup d’œil des objets sur un écran. Cependant, il existe encore une incertitude par rapport à ces données : ces résultats pourraient aussi provenir d’une dysfonction exécutive par exemple, d’un trouble attentionnel freinant la direction de son attention vers les objets saillant.


Le système de suivi d'objets permet de dénombrer rapidement et intuitivement un petit nombre d'objets.

Il existe d’autres théories explicatives de la dyscalculie, qui ont moins d’assises expérimentales. Par exemple, certains chercheurs mettent en lumière l’importance, dans le développement des facultés arithmétiques chez l’enfant, de compter sur ses doigts. Il semble exister, dans certains cas en tout cas, une intrication entre la motricité digitale et les capacités mathématiques, sans qu’un lien de causalité (dans un sens comme dans l’autre) puisse être, à ma connaissance, explicité. Deux grandes observations viennent appuyer cette hypothèse. La première concerne les patients atteints du syndrome de Gertsman, une pathologie très rare, qui est caractérisé à la fois par une acalculie (une incapacité totale de calculer) et une agnosie digitale (perte de connaissance de ses doigts). La seconde concerne plusieurs études qui montrent que les épreuves de gnosie/discrimination digitale en maternelle permettent de prédire les capacités arithmétiques des élèves en CP.

Il existe donc une grande hétérogénéité dans les mécanismes à l’origine d’une dyscalculie. Cette hétérogénéité se manifeste dans les différentes classifications cliniques de la dyscalculie. Par exemple, certains auteurs définissent ainsi une dyscalculie numérique, une dyscalculie des faits arithmétiques (l’incapacité de stocker/repécher les informations arithmétiques) et une dyscalculie dite procédurale (difficultés à planifier et exécuter l’algorithme de calcul dans une opération). Il existe d’autres classifications, qui varient en fonction du cadre théorique dans lequel elles s’inscrivent. Il n’existe pas de réel consensus actuellement sur les sous-types de dyscalculie.

Peu d’études se sont penchées sur le fonctionnement cérébral des enfants ou des adultes dyscalculiques. Les données actuelles tendent à montrer qu’au cours des tâches numériques ou arithmétiques, les régions habituellement activées le sont moins en cas de dyscalculie : c’est le cas par exemple du sillon intra-pariétal, l’une des principales régions impliquées dans les aptitudes mathématiques. Cependant, le “profil” d’activation du cerveau dyscalculique est complexe : ainsi, certaines régions ont tendance à s’activer plus que la normale, par exemple au niveau du cortex préfrontal. Cela s’expliquerait par la nécessiter de recruter plus de ressources cognitives pour résoudre les mêmes tâches arithmétiques. Les études sur le sujet sont peu nombreuses, et il est donc difficile de dessiner une cartographie précise du cerveau dyscalculique. Il est de plus difficile de tracer un lien de causalité entre ces variations de fonctionnement et les difficultés liées à la dyscalculie : le fonctionnement cérébral atypique est-il à l’origine des difficultés mathématiques ? Ou au contraire les difficultés mathématiques entraîneraient elles un remodelage cérébral, secondaire ? Nous ne pouvons trancher actuellement.


Deux régions du cerveau "mathématicien" (ici présenté) ont été incriminées dans la dyscalculie. D'une part, le sillon intra-pariétal (orange), qui a un rôle central dans les aptitudes mathématiques en générale, serait dysfonctionnel dans la dyscalculie. D'autre part, le cortex préfrontal (rose), serait plus fortement recruté (hyperactivé) pour compenser.

Quelle prise en charge ?

La prise en charge de la dyscalculie est importante car sans celle-ci, le trouble a tendance à persister jusqu’à l’âge adulte. C’est particulièrement le cas lorsqu’il existe un autre trouble dys associé (particulièrement la dyslexie).

La dyscalculie est principalement prise en charge par l’orthophoniste, qui pourra évaluer les difficultés et organiser leur prise en charge spécifique. Le suivi peut aussi se focaliser sur les fonctions exécutives, si elles sont particulièrement déficientes et leur impact fort sur la vie quotidienne. Il existe enfin plusieurs applications et serious games qui permettent aux enfants de travailler leurs capacités arithmétiques de façon ludique. On peut citer “La course aux nombres” ou “L’attrape-nombre”, par exemple.

La connaissance de la dyscalculie, et sa prise en charge précoce, apparait fondamentale, car les répercussions des difficultés mathématiques sur la scolarité, la vie quotidienne et le devenir de ces enfants sont importants. Ainsi, une étude anglaise montrait que 70% de ceux-ci quittaient l’école prématurément, et très peu d’entre eux avaient un emploi à temps plein à 30 ans -bien que l'intrication avec d'autres troubles comorbides n'étaient pas claire. Il y a donc tout à gagner à démocratiser ce trouble, afin qu’il soit mieux détecté et mieux accompagné.

Instagram Follow on Instagram

 

SOURCES :

CREDITS PHOTOS :

- Image par Gerd Altmann de Pixabay

- Image par seventhemes de Pixabay

- Image par Clker-Free-Vector-Images de Pixabay

- Image par Colleen de Pixabay

- Par Pancrat — Travail personnel, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=13880070

- Par Pancrat — Travail personnel, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=13558070

- Image par Emmie_Norfolk de Pixabay